Lesson 07

分区Partition

分区思维

思路

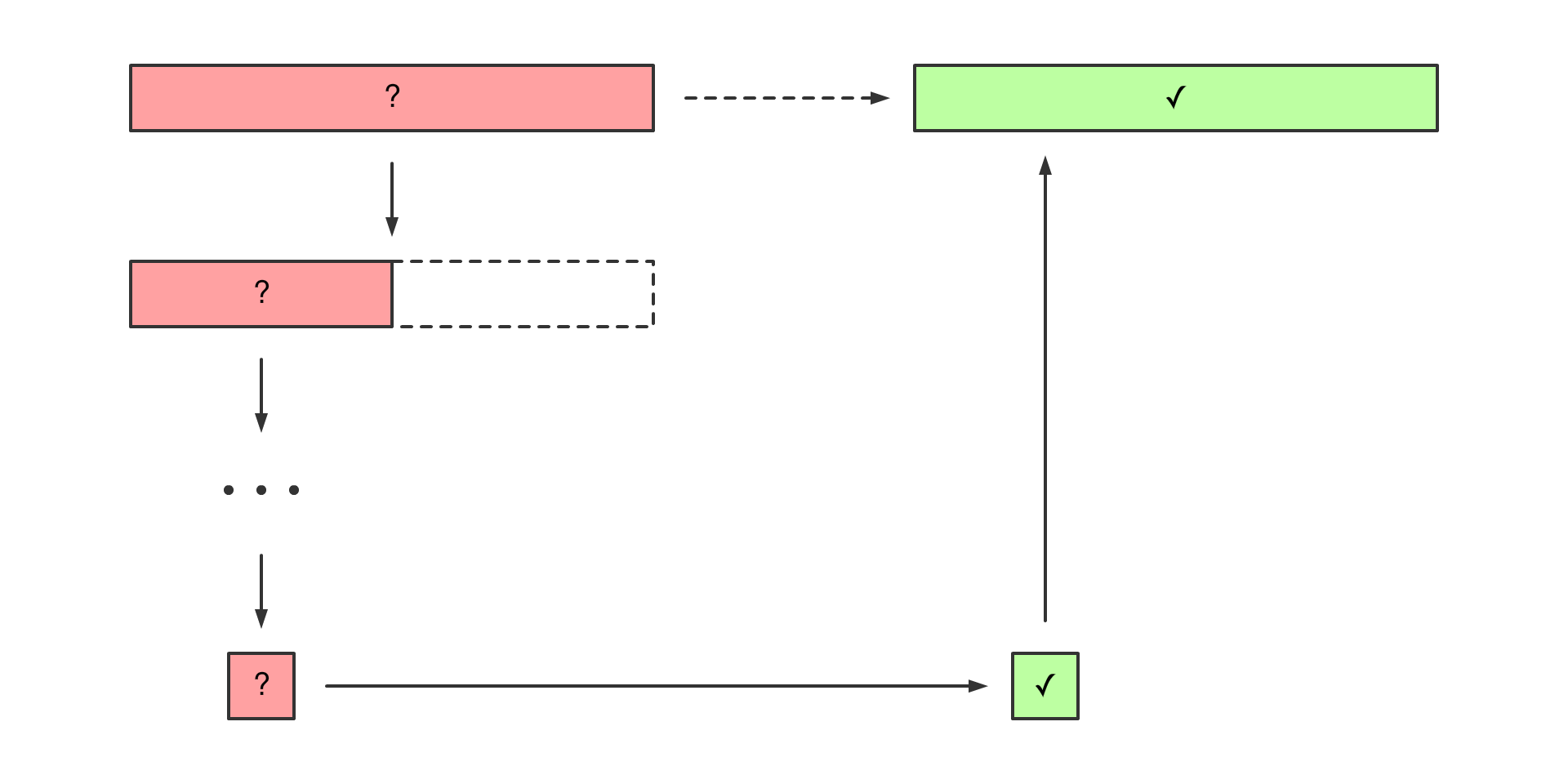
不直接解决问题

转而去想，我能不能把问题拆成 2 个，分别解决，

或者，在有可能的情况下，扔掉 1 个

二叉搜索Binary Search

问题

给定一个升序序列 $A = <A_1, A_2, ... , A_n>$

找到这个序列里是否存在一个数 $q$

任务

代码

时间复杂度分析

递归 Basecase 分析

找相对低的值，尝试，看最后问题都落到了多少规模的。

快速选择QuickSelect

问题

给定一个数组 n

里面不保证排序

6, 1, 7, 8, 2

找到 升序之后 第 k 个数

1, 2, 6, 7, 8

思维

常量降级、倍数降级、分区

方案

6 7 3 8 4 0 9 2 1 5

Partition

1. 选出一个 pivot 点

假设选 第 1 个

2. 使用 pivot 点进行 Partition

3 4 0 2 1 5 6 7 8 9
          < ^ >

Check

3. 比较 Pivot 当前的位置 和 k

when pivot_position > k
when pivot_position < k
when pivot_position = k

Recursion

4. 继续下去

代码

Partition 算法

方案

三个变量 pivot, i, j

arr[j] > pivot 
j++

arr[j] < pivot 
swap(arr, i, j)
i++
j++

时间复杂度分析

最好

arr = 5 1 2 3 4 6 7 8 9 
k = 5                       

第一次 partition 的 中轴点（也就是最左边的点 5）

时间 就是 O(n)

T(n) = O(n) + c
     = O(n)

最差的最好

arr = 5 1 2 3 4 6 7 8 9 
k = 4 

每次 partition 时，pivot 点 都能平分数据

但是 递归到 arr 只剩下一个 的时候，才知道

T(n) = O(n) + T(n/2)
     = O(n)

最差的最差

arr = 1 2 3 4 5 6 7 8 9 
k = 9

升序序列，并且找最后一个

T(n) = O(n) + T(n - 1)
     = O(n^2)

快排QuickSort

思路

如果 partition 能确定 一个数的位置

那么我们两边的数据，可以继续 partition

案例

时间复杂度分析