Lesson 05

训练

特殊情况分析

事实

算法程序的错误

语法错误 / 时间复杂度太高 / 特殊情况没考虑到 / 审题

括号问题

要求

给定一个 非空 字符串 str，

里面由

()[]{}

符号组成。

请你确定是否合法

API

isValid(str: String) : Bool 

分析

一般情况

思路

伪代码

特殊情况

案例

后果

问题所在

修改方案

表达式计算

要求

给定一个 表达式 由 个位整数 和 $+-*/$ 组成

比如：

"3+4*2-1"

求出表达式的结果

API

calculate(expression: String) : Int 

算法

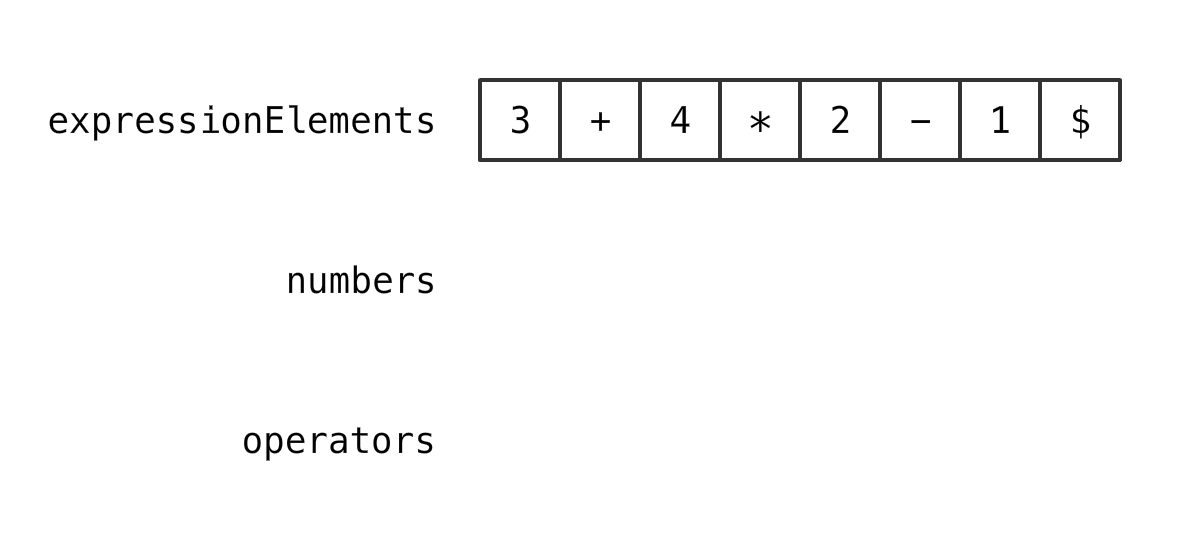
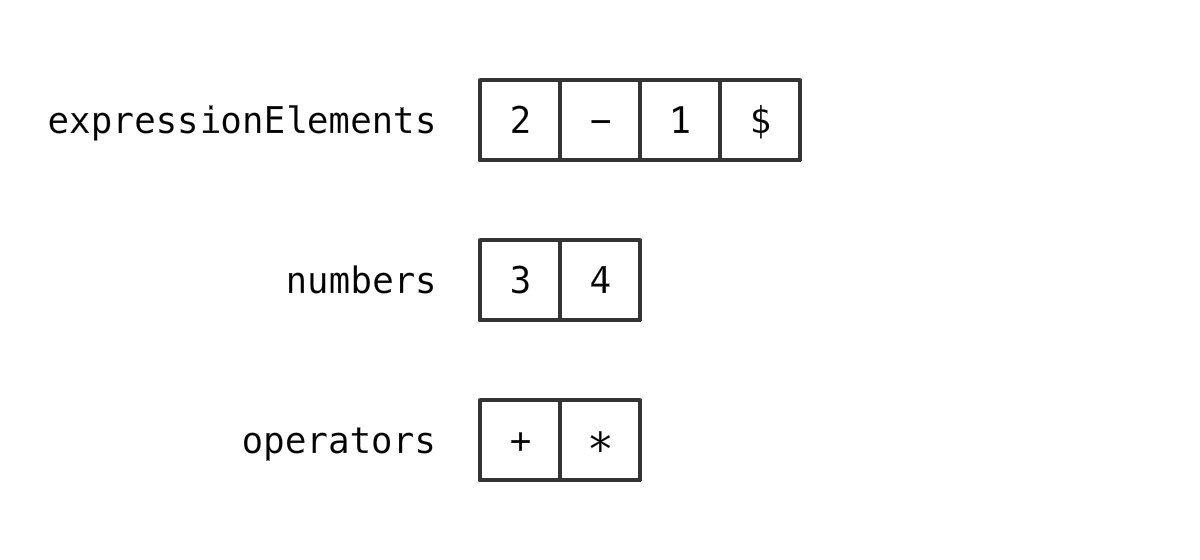
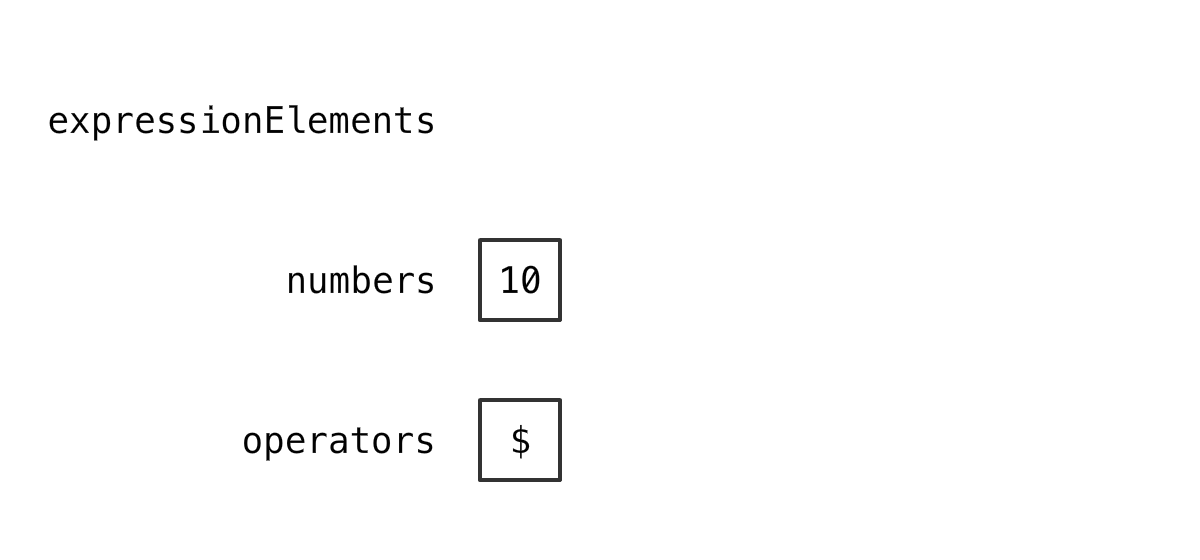
字符串末尾添加 "$"

3+4*2-1
3+4*2-1$

准备两个 Stack

每次拿出两个元素

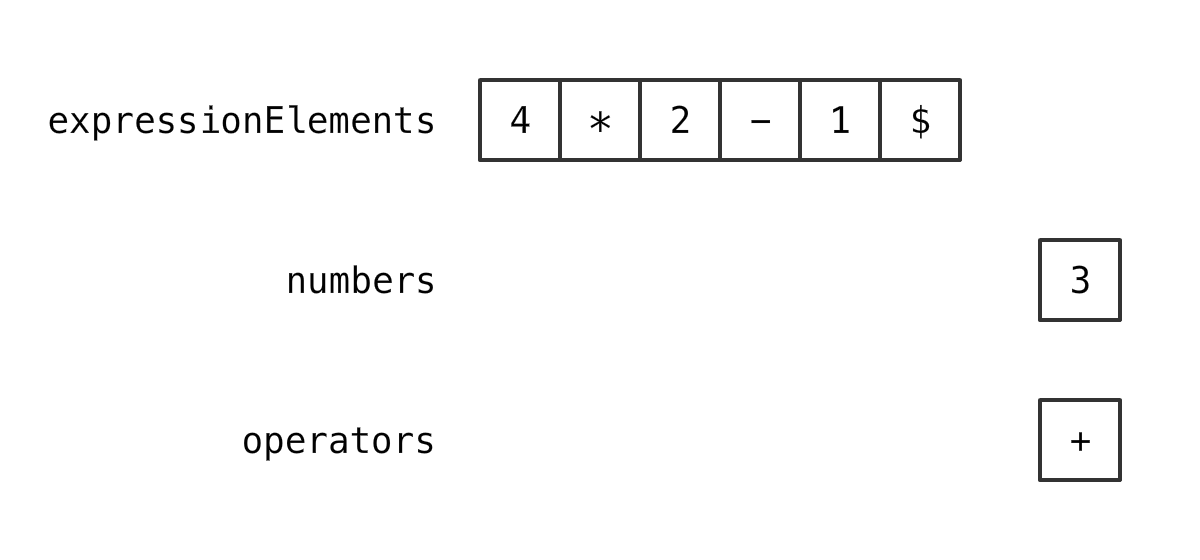
情况 1

如果 stack 为空

那么 放进去

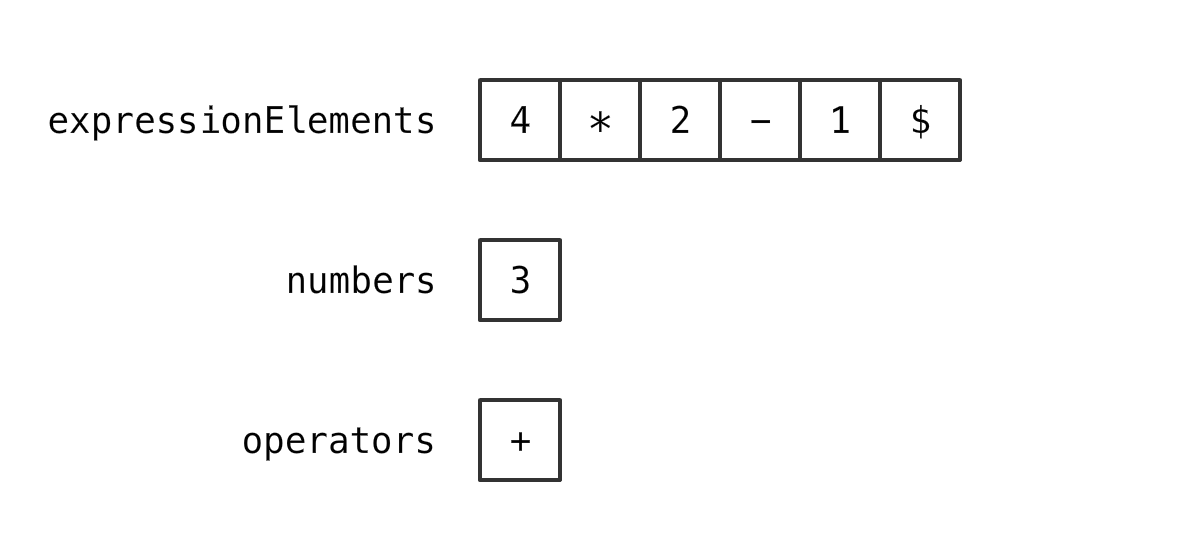
再拿出 两个元素

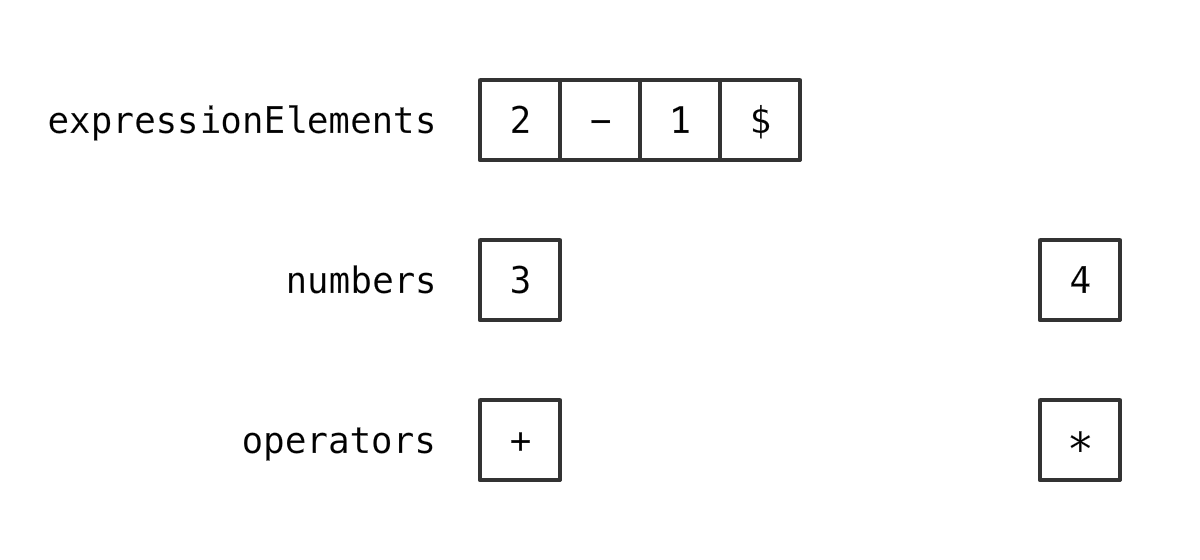
情况 2

如果 新的运算符 优先级 高于 栈顶的运算符 优先级

那么 放进去

再拿出 两个元素

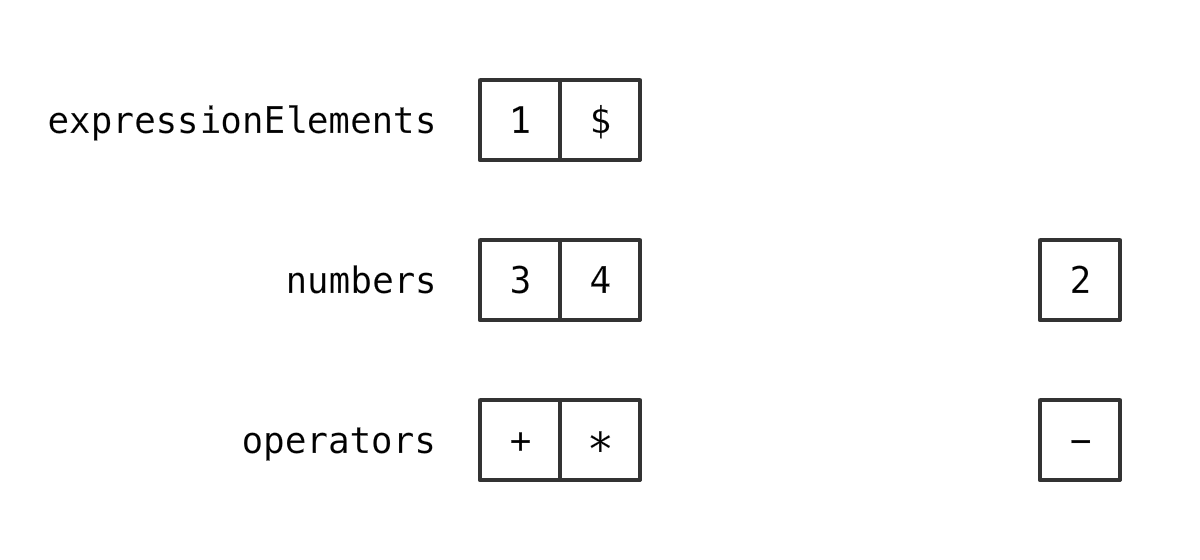
情况 3

如果 新的运算符 优先级 低于 栈顶的运算符 优先级

那么 从两个 Stack 里 各取出 1 个元素

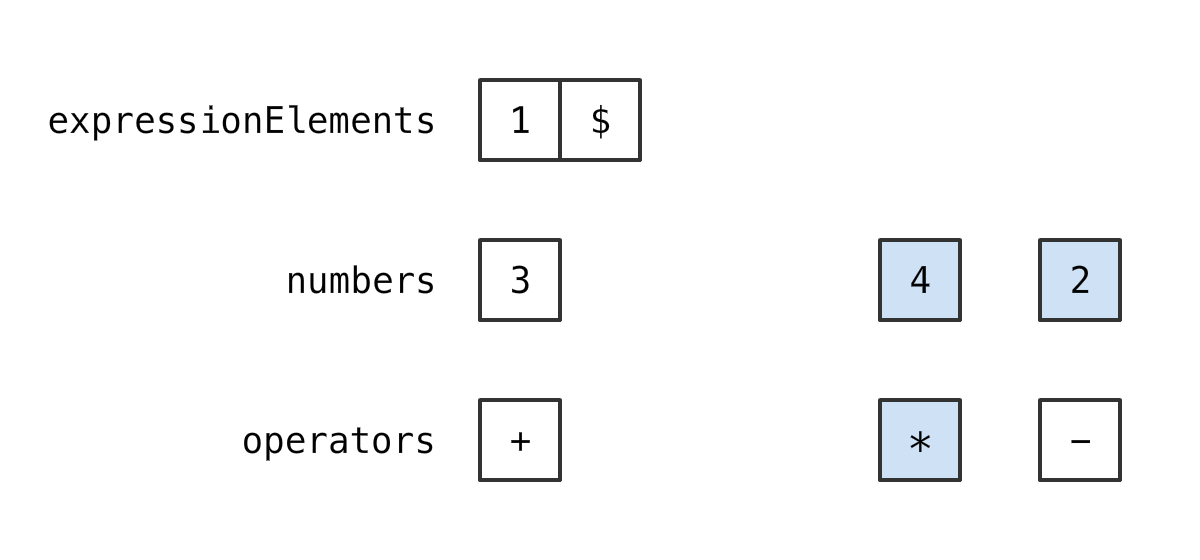
计算

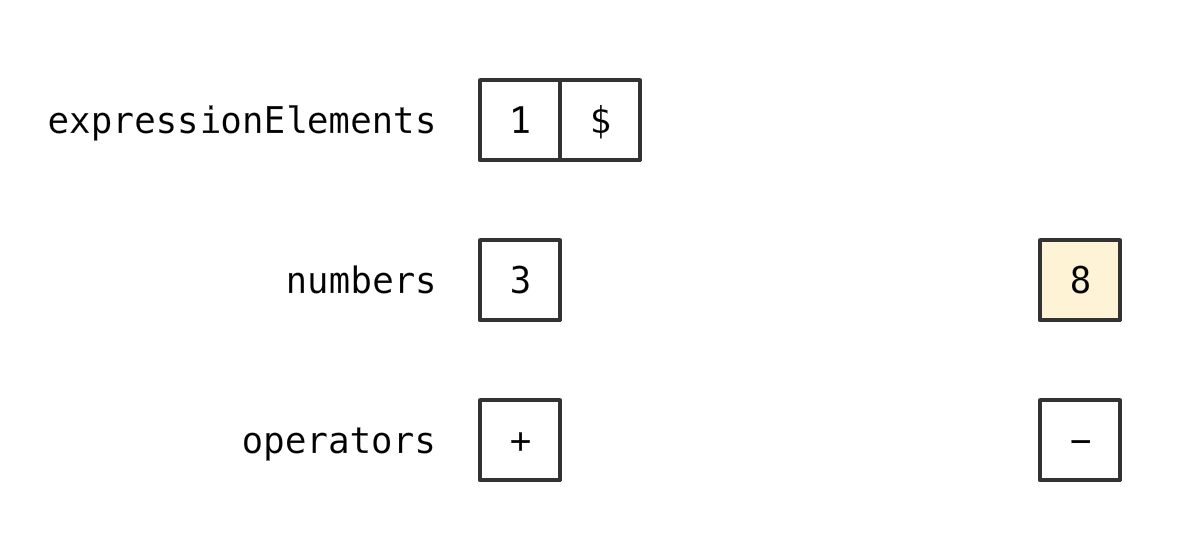
再比较

情况 4

如果 新的运算符 优先级 等于 栈顶的运算符 优先级

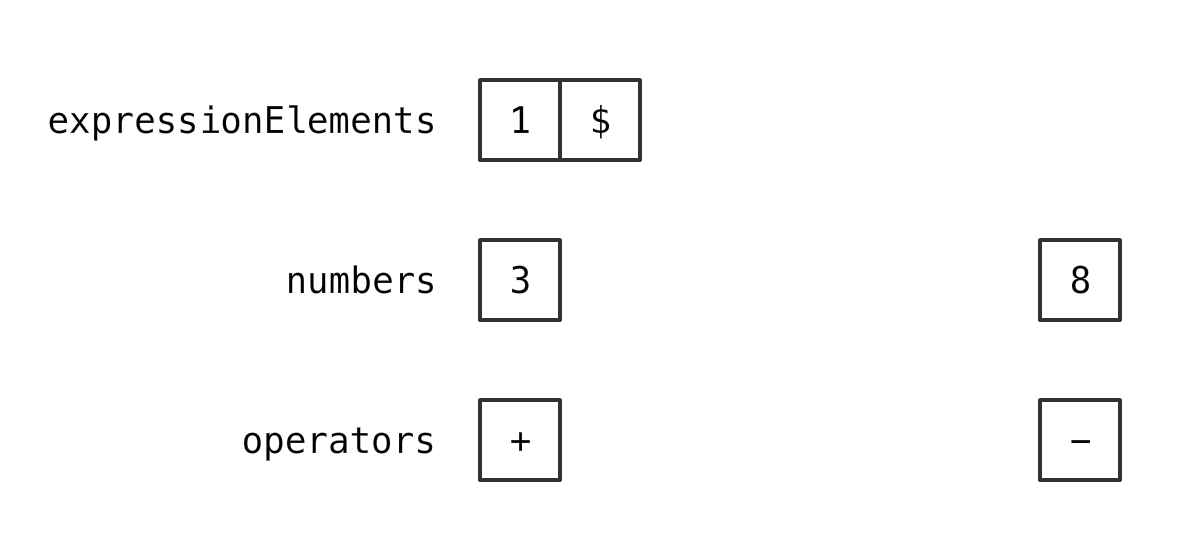
那么 从两个 Stack 里 各取出 1 个元素

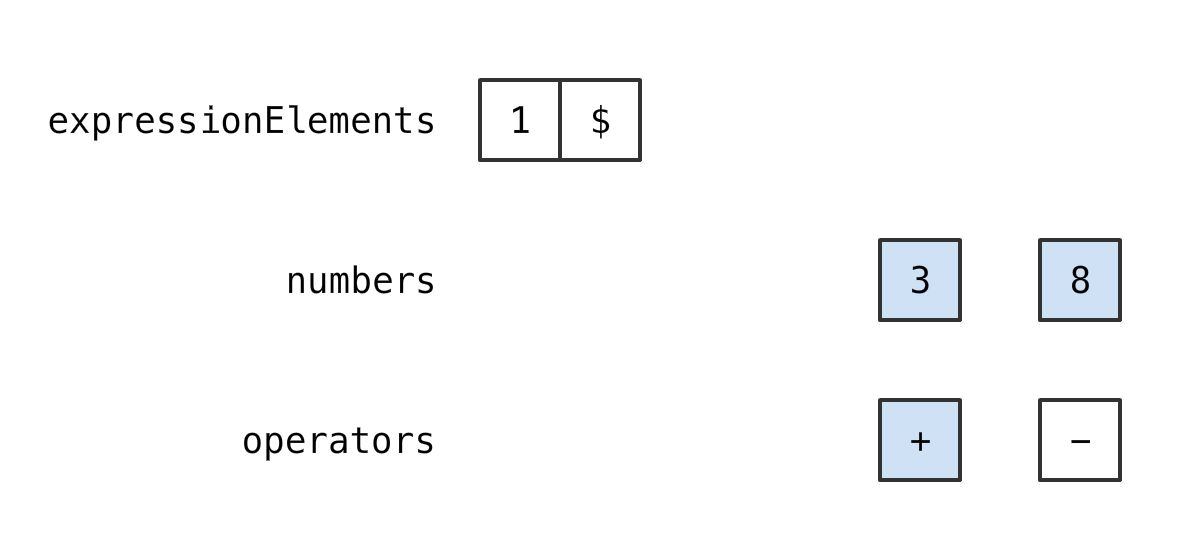
计算

再比较

走下去

情况 1，放进去

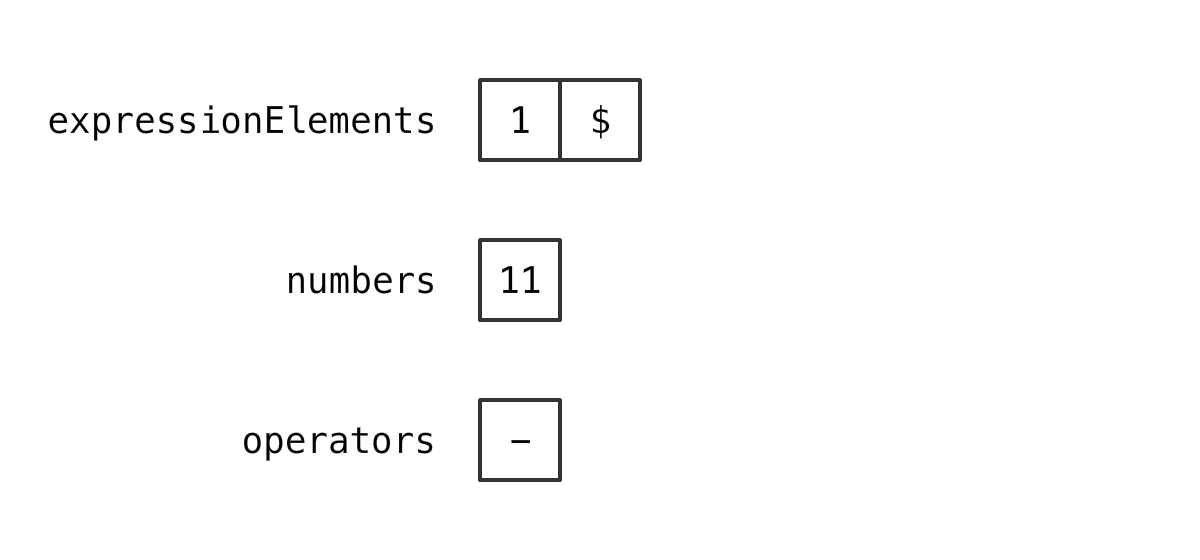
取 2个

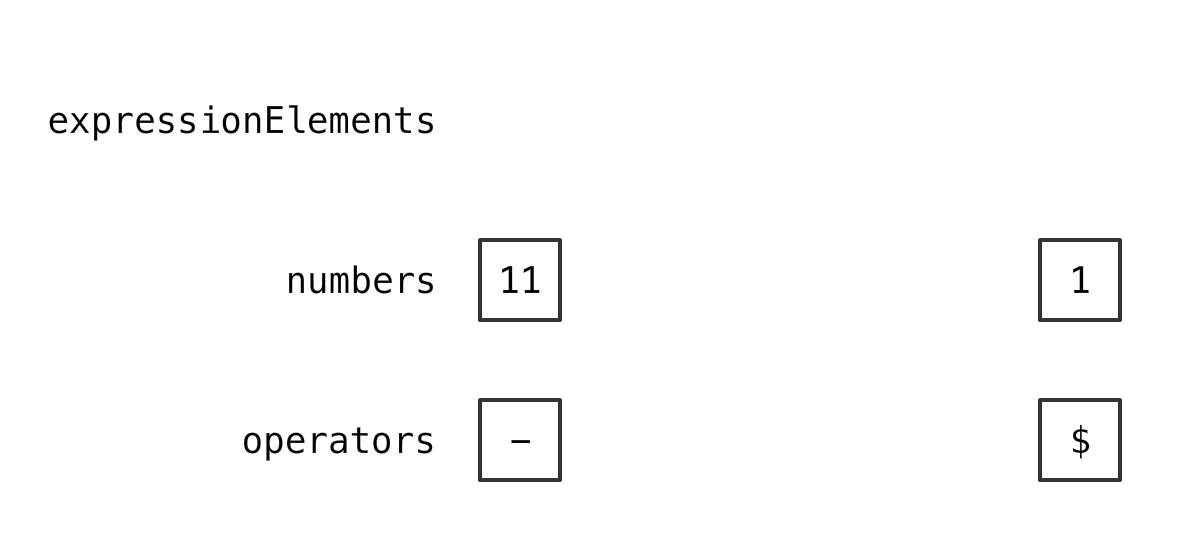
情况 2，各取 1 个

计算

情况 1，放进去

结束

numbers 栈顶元素就是结果

分析

等于的时候为什么要计算，而不是放进去。

递归

递归语法

一个 函数 调自己

1 2 3 4 5 6 7 8 9 10 11 
void run(){    f(3);} void f(int a){    if (a == 0) {        System.out.println("end");    }     f(a - 1);}

递归算法

使用函数递归，解决问题

递归思维

一种全新的思维方式

不直接解决问题

转而去想，如果已经解决了一个小问题，我能不能解决这个大问题

和 数学归纳法 对比

Mathematical Induction

不求 $S(n) = f(n)$

转而去求 $S(n) = f(S(n - 1))$

常量降级

套路

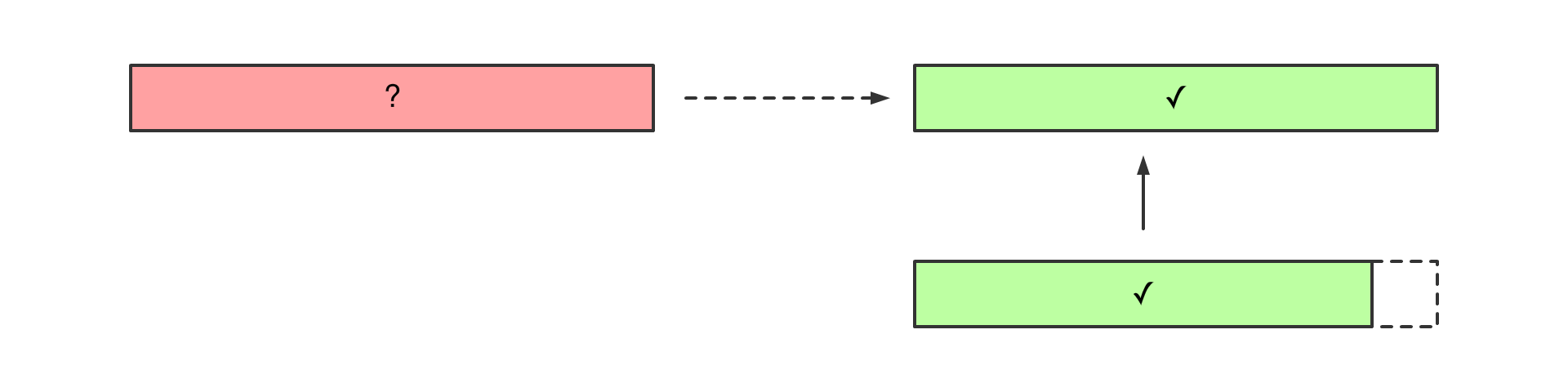
假设 你已经拿到了 n - 1 的问题的答案

想一下 是否可以通过这个答案 解决 n 的问题的答案

思路案例

问题

求 n 个数的 最大值

对照表

思路

假设 我已经知道了 n - 1 个数 的最大值，

想一下 是否可以通过 这个值 求出 n 个数 的最大值呢

答案

可以

训练

求 2 的 n 次方

递归重要元素

1. 递归

当 $n > 1$ 时

$ArrayMax(A, n) = max(ArrayMax(A, n - 1), A_n)$

2. base case

当 $n = 1$ 时

$ArrayMax(A, n) = A_n$

训练

求 2 的 n 次方

时间复杂度分析

案例

$Power2(n)$

    $\text{if } n = 1 \text{ then}$

        $\text{return } 2$

    $\text{return } Power2(n - 1) * 2;$

分段分析

$T(n) = O(1)         \text{ when } n = 1$

       $T(n - 1) + c \text{ when } n > 1$

代数

$T(n) = c + T(n - 1)$

     $= c + (c + T(n - 2))$

     $= c + (c + (c + T(n - 3)))$

     $= ...$

     $= c + c + c + ... + c + O(1)$

     $= c + c + c + ... + c + c_2$

     $= cn + c_2$

     $= O(n)$