Lesson 02
时间复杂度Time Complexity
案例
方法 1
找到所有 两个数 配对的可能
保留最高值
伪代码
Max2Sum(A,n)
sum←0
for i←1 to n
for j←1 to n
if i!=j then
if Ai+ij>sum then
sum=Ai+Aj
return sum
方法 2
循环一遍 找到最大值
再循环一遍 找到第二个大的值
伪代码
Max2Sum(A,n)
max1←0
for i←1 to n
if Ai>max1 then
max1←Ai
max2←0
for i←1 to n
if Ai>max2 and Ai!=max1 then
max2←Ai
return max1+max2
方法 3
跟方法 2 一样,但只走一趟
伪代码
Max2Sum(A,n)
max1←0
max2←0
for i←1 to n
if Ai>max2 then
max2←Ai
if Ai>max1 then
Swap(max1,max2)
return max1+max2
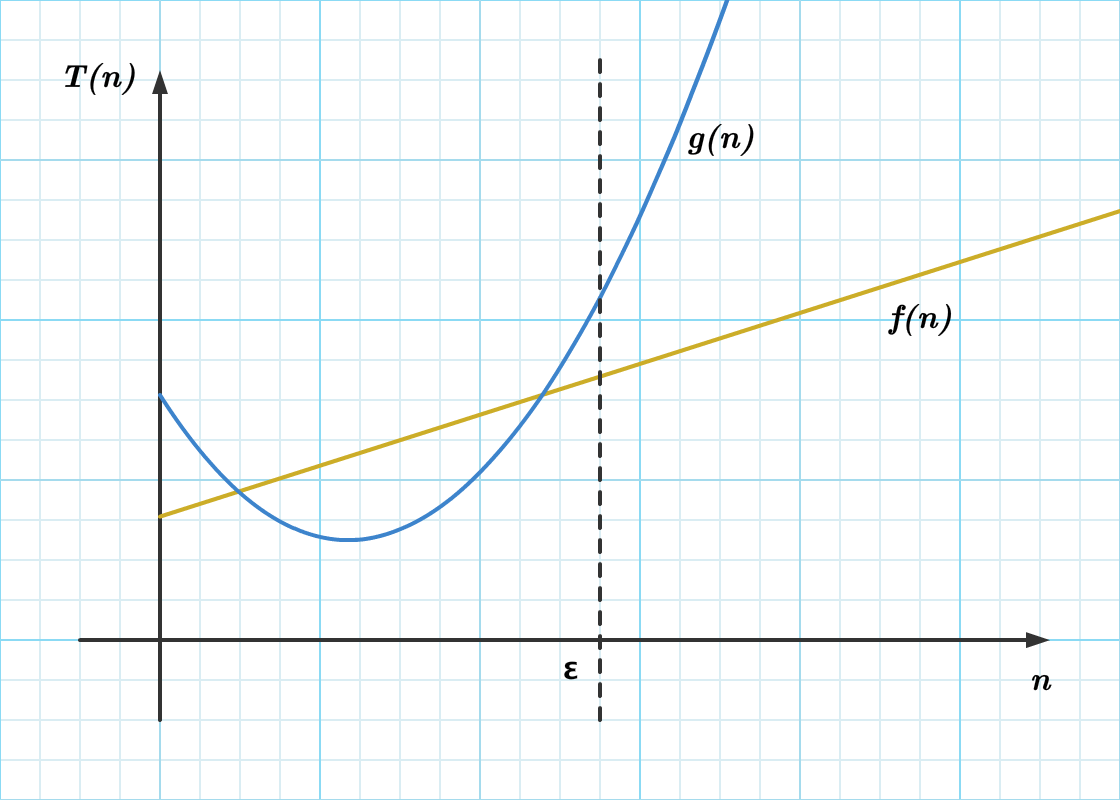
相对优势 与 绝对优势
大于 某个值之后
我们比较大于某个值 ϵ 后面的
相对优势
什么是
通过对 时间公式 叠加 常量倍数 会影响比较结果
案例
| n=10,c=1 | 10 | 20 | f(n) |
| n=100,c=1 | 100 | 200 | f(n) |
| n=10,c=1/10 | 10 | 2 | g(n) |
| n=100,c=1/10 | 100 | 20 | g(n) |
实际
如果设备一样 那么一个比一个好
但是可以通过砸钱在硬件设备上,彻底改变结果
函数图
∃ ϵ>0
when n>ϵ and n→∞
∃ c1>0,c1⋅g(n)≥f(n) and
∃ c2>0,f(n)≥c2⋅g(n)
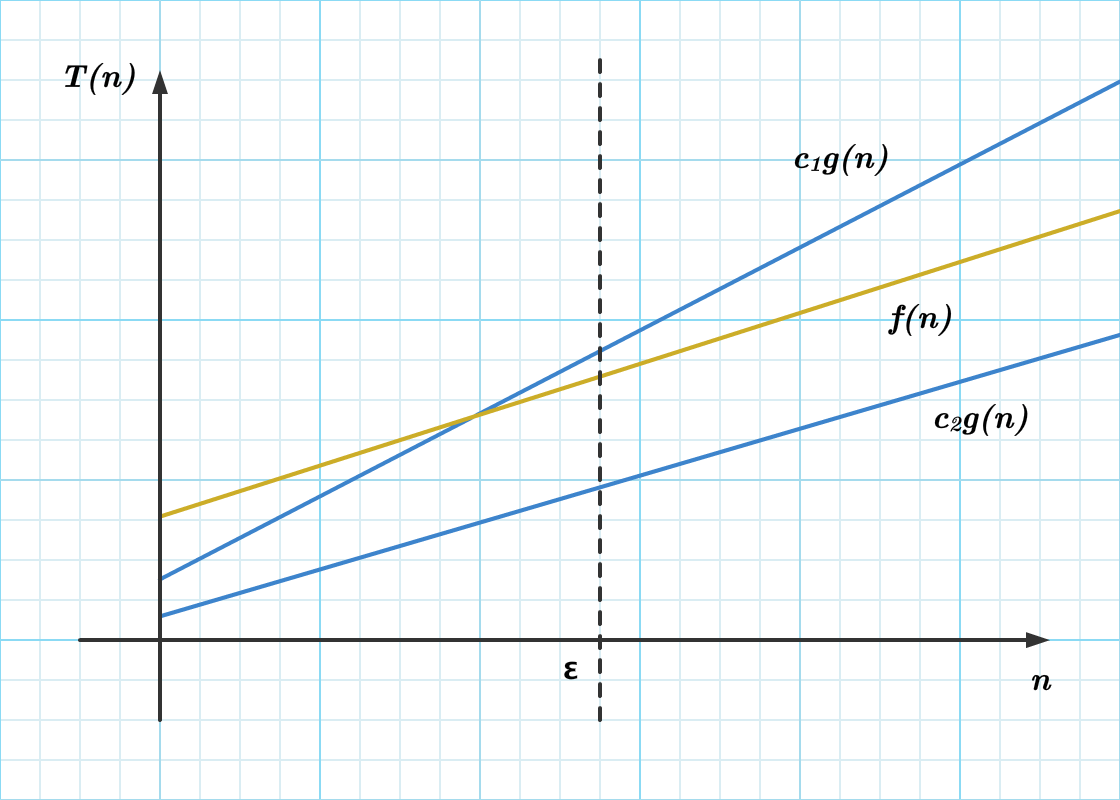
绝对优势
什么是
通过对 时间公式 叠加 常量倍数 不会 影响比较结果
案例
| n=2,c=1 | 2 | 4 | f(n) |
| n=2,c=1/10 | 2 | 0.4 | g(n) |
| n=20,c=1/10 | 20 | 40 | f(n) |
| n=20,c=1/100 | 20 | 4 | g(n) |
| n=200,c=1/100 | 200 | 400 | f(n) |
| n=200,c=1/1000 | 200 | 40 | g(n) |
实际
就算通过砸钱在硬件设备上,当数据量大时也无法改变结果
函数图
∀ c>0
∃ ϵ>0
when n>ϵ and n→∞
c⋅g(n)≥f(n) and
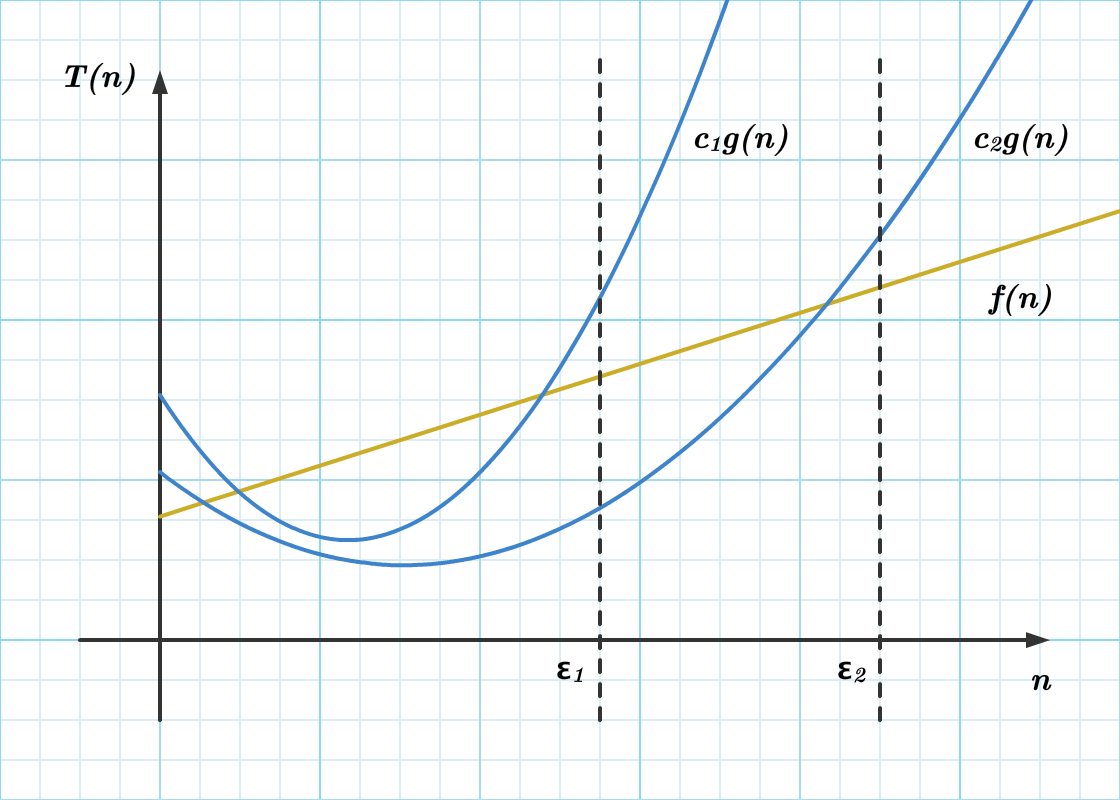
优势研究
侧重点
应该优先专注 提高绝对优势
代码可读性
当只有相对优势时,我们可以 专注代码可读性
速度档位
速度档位
相同档位
互相有相对优势的时间函数,被归类到一个速度档位内,他们的时间复杂度一样
n 和 2n 就在一个档位,时间复杂度一样
不同档位
有绝对优势的时间函数,就不会再一个速度档位上,他们的时间复杂度也不一样
| n | 时间增长慢 | 低档位 | 时间复杂度低 | 更好 |
| n2 | 时间增长快 | 高档位 | 时间复杂度高 | 不好 |
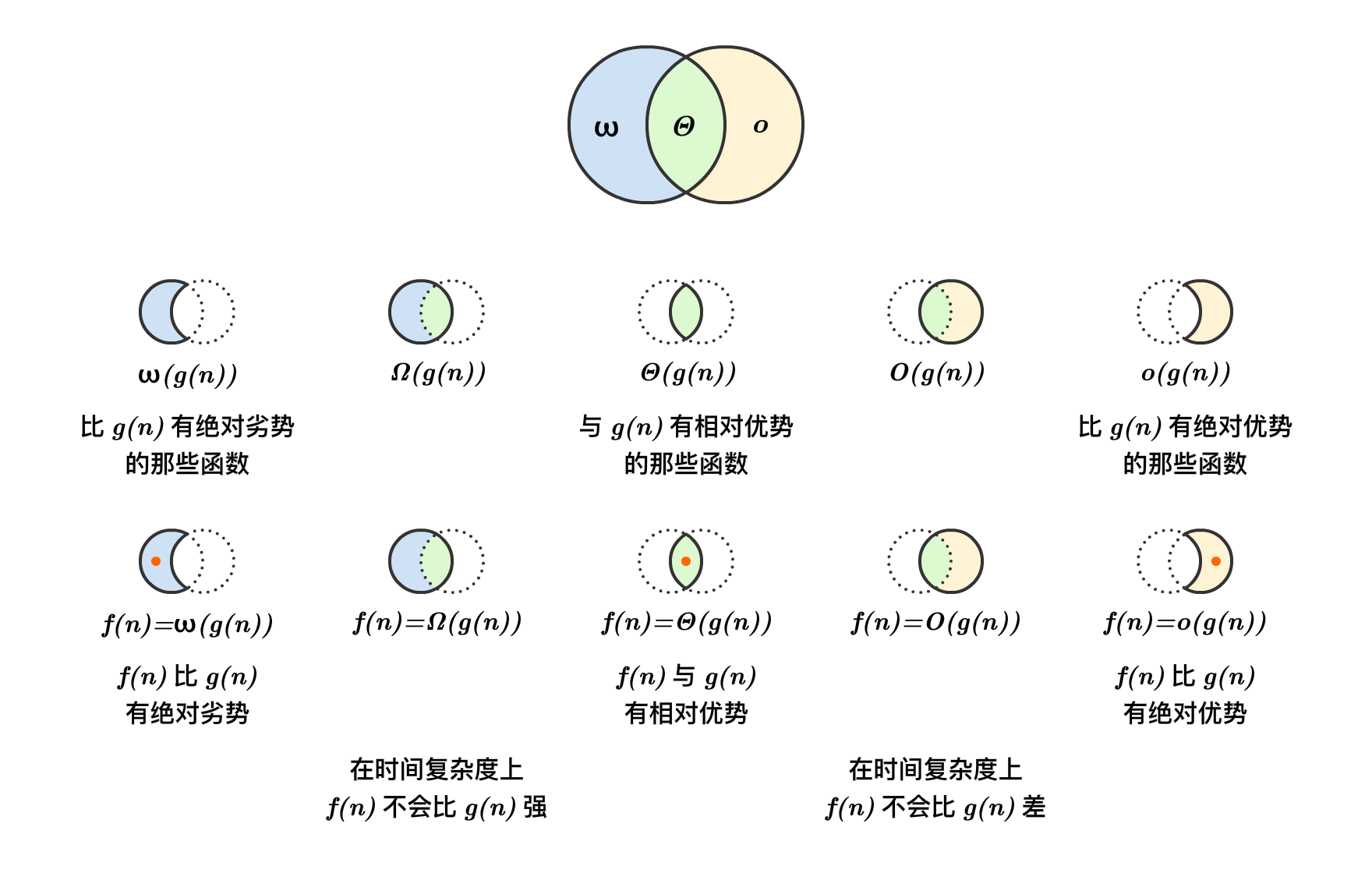
Θ(n)
什么是
如果 T1(n)=f(n) 和 T2(n)=g(n) 在一个速度档位上
就说 f(n)=Θ(g(n))
含义
意思就是 f(n) 与 g(n) 档位相同
集合含义
Θ(g(n)) 代表 跟 g(n) 档位 相同的那些函数 所组成的集合
那么 f(n)=Θ(g(n))
意思就是 f(n)∈Θ(g(n))
样例
n=Θ(n)
n=Θ(2n)
O(n)
什么是
如果 T1(n)=f(n) 和 T2(n)=g(n) 在一个速度档位上
或者 T1(n)=f(n) 比 T2(n)=g(n) 有绝对优势
就说 f(n)=O(g(n))
含义
意思就是 f(n) 档位 差不过 g(n)
集合含义
O(g(n)) 代表 跟 g(n) 档位 相同 以及 更好 的那些函数 所组成的集合
那么 f(n)=O(g(n))
意思就是 f(n)∈O(g(n))
样例
n=O(n)
n=O(n2)
Θ(n) 与 O(n) 对比
如果 f(n) = \Theta(g(n)),那么 f(n) = O(g(n))。
不能反过来。
练习
以下哪个是对的
1. n=Θ(n)
2. n=Θ(2n)
3. 2n=Θ(n)
4. n=Θ(n2)
5. n2=Θ(n)
6. n=O(n)
7. n=O(2n)
8. 2n=O(n)
9. n=O(n2)
10. n2=O(n)
完整对比
相关推论 与 常用数学公式
证明档位
limn→∞g(n)f(n)
| 1 | 档位一样 |
| 0 | f(n) 比 g(n) 有绝对优势 |
| ∞ | g(n) 比 f(n) 有绝对优势 |
多项式后面抹除
如果时间公式为一个多项式,只需要保留最高档位的部分
比如
T(n)=n2+2n+1=O(n2)
常量系数抹除
如果时间公式为乘积,可以抹除常量系数
比如
T(n)=3n2=O(n2)
log 相关公式
a,b,c 均为常数
去底
logan=logcalogcn=logca1⋅logcn=O(logcn)=O(logn)
去幂
logna=alogn=O(logn)
去系数
logabn=logab+logan=O(logan)=O(logn)
档位列表
O(1)=O(c)<O(logn)<O(n)<O(nlogn)<O(n2)<O(nc)<O(cn)